Ikoct的饮冰室
0%

NBCTF2024逆向方向wp

发表于 更新于 分类于 ，
本文字数： 18k 阅读时长 ≈ 17 分钟

参赛ID:1K0CT

Crisscross | pyre

给了一个python程序和它的输出:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import random

key1 = random.choices(range(256), k=20)
key2 = list(range(256))
random.shuffle(key2)
flag = open('flag.txt', 'rb').read()    

def enc(n):
    q = key2[n]
    w = key1[q % 20]
    n ^= q
    return n, w

x = 0
for i, c in enumerate(flag):
    x <<= 8
    n, w = enc(c)
    if i % 2:
        n, w = w, n
    x |= n
    x |= w << ((2 * i + 1) * 8)

print(key1)
print(key2)
print(x)
#[127, 81, 241, 40, 222, 128, 45, 87, 27, 154, 66, 162, 73, 176, 172, 164, 106, 234, 77, 5]
#[155, 117, 124, 113, 104, 46, 151, 71, 144, 229, 152, 240, 199, 88, 103, 105, 245, 209, 13, 82, 166, 9, 201, 233, 228, 154, 19, 5, 30, 141, 81, 206, 246, 232, 107, 29, 208, 253, 187, 116, 98, 160, 60, 7, 220, 143, 80, 239, 52, 15, 94, 50, 149, 241, 57, 92, 230, 100, 31, 51, 36, 24, 39, 14, 25, 90, 101, 55, 194, 225, 157, 102, 2, 26, 148, 161, 180, 120, 223, 165, 32, 146, 185, 243, 119, 210, 172, 244, 1, 125, 44, 35, 169, 179, 188, 64, 207, 33, 137, 200, 142, 182, 250, 195, 28, 4, 79, 191, 86, 215, 96, 236, 91, 122, 196, 87, 118, 231, 126, 97, 147, 67, 132, 190, 234, 237, 43, 193, 252, 18, 212, 163, 56, 73, 123, 176, 162, 23, 192, 49, 21, 242, 171, 112, 153, 238, 203, 134, 167, 93, 115, 95, 8, 12, 65, 217, 248, 168, 219, 47, 211, 108, 76, 129, 145, 62, 156, 34, 218, 135, 48, 70, 75, 3, 249, 72, 202, 133, 183, 38, 37, 227, 164, 173, 159, 251, 0, 174, 54, 20, 136, 53, 138, 99, 226, 178, 42, 66, 150, 205, 204, 214, 197, 235, 110, 216, 63, 45, 184, 74, 41, 177, 27, 69, 130, 89, 61, 247, 255, 17, 254, 181, 131, 22, 224, 83, 189, 59, 114, 139, 111, 68, 6, 84, 11, 127, 221, 106, 77, 109, 158, 170, 16, 121, 222, 186, 10, 58, 175, 40, 128, 198, 78, 85, 213, 140]
#3449711664888782790334923396354433085218951813669043815144799745483347584183883892868078716490762334737115401929391994359609927294549975954045314661787321463018287415952

求出flag每一位对应的(w, n)(需要注意的是w和n的排列顺序类似...n[2], w[1], n[0], w[0], n[1], w[1]...) 再稍微改一下原程序爆破出flag:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
key1 = [127, 81, 241, 40, 222, 128, 45, 87, 27, 154, 66, 162, 73, 176, 172, 164, 106, 234, 77, 5]
key2 = [155, 117, 124, 113, 104, 46, 151, 71, 144, 229, 152, 240, 199, 88, 103, 105, 245, 209, 13, 82, 166, 9, 201, 233, 228, 154, 19, 5, 30, 141, 81, 206, 246, 232, 107, 29, 208, 253, 187, 116, 98, 160, 60, 7, 220, 143, 80, 239, 52, 15, 94, 50, 149, 241, 57, 92, 230, 100, 31, 51, 36, 24, 39, 14, 25, 90, 101, 55, 194, 225, 157, 102, 2, 26, 148, 161, 180, 120, 223, 165, 32, 146, 185, 243, 119, 210, 172, 244, 1, 125, 44, 35, 169, 179, 188, 64, 207, 33, 137, 200, 142, 182, 250, 195, 28, 4, 79, 191, 86, 215, 96, 236, 91, 122, 196, 87, 118, 231, 126, 97, 147, 67, 132, 190, 234, 237, 43, 193, 252, 18, 212, 163, 56, 73, 123, 176, 162, 23, 192, 49, 21, 242, 171, 112, 153, 238, 203, 134, 167, 93, 115, 95, 8, 12, 65, 217, 248, 168, 219, 47, 211, 108, 76, 129, 145, 62, 156, 34, 218, 135, 48, 70, 75, 3, 249, 72, 202, 133, 183, 38, 37, 227, 164, 173, 159, 251, 0, 174, 54, 20, 136, 53, 138, 99, 226, 178, 42, 66, 150, 205, 204, 214, 197, 235, 110, 216, 63, 45, 184, 74, 41, 177, 27, 69, 130, 89, 61, 247, 255, 17, 254, 181, 131, 22, 224, 83, 189, 59, 114, 139, 111, 68, 6, 84, 11, 127, 221, 106, 77, 109, 158, 170, 16, 121, 222, 186, 10, 58, 175, 40, 128, 198, 78, 85, 213, 140]
x = 3449711664888782790334923396354433085218951813669043815144799745483347584183883892868078716490762334737115401929391994359609927294549975954045314661787321463018287415952
flag = []
while(x):
    flag.append(x & 0xFF)
    x >>= 8
w_o = []
n_o = []
for i in range(35):
    n_o.append(flag[35 + (-1 if ((i + 1) % 2) else 1) * ((2 * int(i / 2) + 1))])
    w_o.append(flag[35 + (-1 if (i % 2) else 1) * int((i + 1) / 2) * 2])
def enc(n):
    q = key2[n]
    w = key1[q % 20]
    n ^= q
    return n, w

i = 0
flag = ''
for _ in range(35):
    for c in range(33, 125):
        n, w = enc(c)
        if n == n_o[i] and w == w_o[i]:
            flag += chr(c)
            i += 1
            break
print(flag, end='')
print("}")
# nbctf{cr15s_cr0ss_str4wb3rry_s4uz3}

Shifty Sands | 进阶的迷宫题

用DIE打开附件 64位ELF无壳 IDA64打开 主函数结构非常简单 胜利的判断是走到L 失败的判定是走到S 唯一需要费点时间看的是加了点混淆(永真判断)的change()函数:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
__int64 __fastcall main(__int64 a1, char **a2, char **a3)
{
  char input; // [rsp+Fh] [rbp-11h]
  int row; // [rsp+10h] [rbp-10h] BYREF
  unsigned int col; // [rsp+14h] [rbp-Ch] BYREF
  unsigned __int64 v7; // [rsp+18h] [rbp-8h]

  v7 = __readfsqword(0x28u);
  row = 0;
  col = 0;
  do
  {
    do
      input = getchar();
    while ( input == 10 );
    change();                                   // 从1开始算
                                                // 走到4n    步时S向右扩散
                                                // 走到4n + 3步时S向上扩散
                                                // 走到4n + 2步时S向左扩散
                                                // 走到4n + 1步时S向下扩散
    ++step;
    check(input, &row, &col);
    if ( step > 49 || maze[10 * row + col] == 'S' )
    {
      puts("ssssssssss");
      return 1LL;
    }
  }
  while ( maze[10 * row + col] != 'L' );
  openflag();
  return 0LL;
}
// change():
unsigned __int64 change()
{
  unsigned __int64 result; // rax
  int jj; // [rsp+0h] [rbp-10h]
  int ii; // [rsp+0h] [rbp-10h]
  int k; // [rsp+0h] [rbp-10h]
  int j; // [rsp+0h] [rbp-10h]
  int kk; // [rsp+4h] [rbp-Ch]
  int n; // [rsp+4h] [rbp-Ch]
  int m; // [rsp+4h] [rbp-Ch]
  int i; // [rsp+4h] [rbp-Ch]

  result = (step % 4);
  if ( result == 3 )
  {
    for ( i = 9; i >= 0; --i )
    {
      for ( j = 0; j <= 9; ++j )
      {
        result = maze[10 * j + i];
        if ( result == 'S' )
        {
          result = j;
          if ( j >= 0 )
          {
            result = (i + 1);
            if ( (result & 0x80000000) == 0LL )
            {
              result = (i + 1);
              if ( result <= 9 )
              {
                result = maze[10 * j + 1 + i];
                if ( result == '.' )
                {
                  maze[10 * j + i] = '.';
                  result = &maze[10 * j + 1 + i];
                  *result = 'S';
                }
              }
            }
          }
        }
      }
    }
  }
  else if ( result <= 3 )
  {
    if ( result == 2 )
    {
      for ( k = 0; k <= 9; ++k )
      {
        for ( m = 0; m <= 9; ++m )
        {
          result = maze[10 * k + m];
          if ( result == 'S' )
          {
            result = (k - 1);
            if ( (result & 0x80000000) == 0LL )
            {
              result = (k - 1);
              if ( result <= 9 )
              {
                result = m;
                if ( m >= 0 )
                {
                  result = maze[10 * k - 10 + m];
                  if ( result == '.' )
                  {
                    maze[10 * k + m] = '.';
                    result = &maze[10 * k - 10 + m];
                    *result = 'S';
                  }
                }
              }
            }
          }
        }
      }
    }
    else if ( result )
    {
      if ( result == 1 )
      {
        for ( n = 0; n <= 9; ++n )
        {
          for ( ii = 0; ii <= 9; ++ii )
          {
            result = maze[10 * ii + n];
            if ( result == 'S' )
            {
              result = ii;
              if ( ii >= 0 )
              {
                result = (n - 1);
                if ( (result & 0x80000000) == 0LL )
                {
                  result = (n - 1);
                  if ( result <= 9 )
                  {
                    result = maze[10 * ii - 1 + n];
                    if ( result == '.' )
                    {
                      maze[10 * ii + n] = '.';
                      result = &maze[10 * ii - 1 + n];
                      *result = 'S';
                    }
                  }
                }
              }
            }
          }
        }
      }
    }
    else
    {
      for ( jj = 9; jj >= 0; --jj )
      {
        for ( kk = 0; kk <= 9; ++kk )
        {
          result = maze[10 * jj + kk];
          if ( result == 'S' )
          {
            result = (jj + 1);
            if ( (result & 0x80000000) == 0LL )
            {
              result = (jj + 1);
              if ( result <= 9 )
              {
                result = kk;
                if ( kk >= 0 )
                {
                  result = maze[10 * jj + 10 + kk];
                  if ( result == '.' )
                  {
                    maze[10 * jj + kk] = '.';
                    result = &maze[10 * jj + 10 + kk];
                    *result = 'S';
                  }
                }
              }
            }
          }
        }
      }
    }
  }
  return result;
}

既然是会动的迷宫 那盯着看原来的迷宫看是几乎不可能解出来的 这里提供一个python程序模仿迷宫的运作并记录步数:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
def print_maze(maze, player_pos):
    for i, row in enumerate(maze):
        for j, cell in enumerate(row):
            if (i, j) == player_pos:
                print('$', end='')
            else:
                print(cell, end='')
        print()
def move_player(maze, direction, player_pos):
    row, col = player_pos
    if direction == 'w' and row > 0 and maze[row - 1][col] != '#':
        maze[row][col], maze[row - 1][col] = maze[row - 1][col], maze[row][col]
        return (row - 1, col)
    elif direction == 's' and row < len(maze) - 1 and maze[row + 1][col] != '#':
        maze[row][col], maze[row + 1][col] = maze[row + 1][col], maze[row][col]
        return (row + 1, col)
    elif direction == 'a' and col > 0 and maze[row][col - 1] != '#':
        maze[row][col], maze[row][col - 1] = maze[row][col - 1], maze[row][col]
        return (row, col - 1)
    elif direction == 'd' and col < len(maze[0]) - 1 and maze[row][col + 1] != '#':
        maze[row][col], maze[row][col + 1] = maze[row][col + 1], maze[row][col]
        return (row, col + 1)
    return player_pos

def spread_sands(maze, step):
    rows, cols = len(maze), len(maze[0])
    if step % 4 == 0:
      for i in range(rows - 1, -1, -1):
        for j in range(cols):
          if maze[i][j] == 'S':
            if i < rows - 1 and maze[i + 1][j] == 'o':
                maze[i][j], maze[i + 1][j] = maze[i + 1][j], maze[i][j]
    elif step % 4 == 3:
      for j in range(cols - 1, -1, -1):
        for i in range(rows):
          if maze[i][j] == 'S':
            if j < cols - 1 and maze[i][j + 1] == 'o':
                maze[i][j], maze[i][j + 1] = maze[i][j + 1], maze[i][j]

    elif step % 4 == 2:
      for i in range(rows):
        for j in range(cols):
          if maze[i][j] == 'S':
            if i > 0 and maze[i - 1][j] == 'o':
                maze[i][j], maze[i - 1][j] = maze[i - 1][j], maze[i][j]
    elif step % 4 == 1:
      for i in range(rows):
        for j in range(cols):
          if maze[i][j] == 'S':
            if j > 0 and maze[i][j - 1] == 'o':
                maze[i][j], maze[i][j - 1] = maze[i][j - 1], maze[i][j]

def main():
    maze_str = """o###ooooo#
                  oo#So##oo#
                  #oS#o#SSo#
                  #oo#o#oo##
                  oSo#o#oSSo
                  o###o#oSoo
                  ooo#o#oooS
                  ##o#o####o
                  oSoSo#ooSo
                  ooSoo#LSoo"""

    maze = [list(row.strip()) for row in maze_str.split('\n')]
    player_pos = (0, 0)
    step = 0
    while maze[player_pos[0]][player_pos[1]] != 'L':
        print_maze(maze, player_pos)
        print(f"Step: {step}")
        print()
        direction = input("Enter your move (w/a/s/d): ")
        player_pos = move_player(maze, direction, player_pos)
        spread_sands(maze, step)
        step += 1
    print("WIN")

if __name__ == "__main__":
    main()

但是因为我的移动逻辑是交换 所以程序还是有点瑕疵(你不会赢 也不会似) 但是作为一个做出答案的辅助工具还是足够的

另外需要注意的是 附件中的迷宫运作逻辑是:

  1. S移动
  2. 玩家所在行, 列变化
  3. 判断玩家所在行, 列是否是S

所以其实是可以实现类似居合和见切的效果的(玩太刀玩的) 不然也无法通关 e.g.

1
2
3
        →		→
↓$    √	$o	√	So	√
↑S       ↑S	   ↑$

最后得到路线后nc到官方的端口并输入路线 得到flag:nbctf{5lowly_5huffl3d 5wa110wing_54nd5}

Itchy Scratchy | Scratch编程逆向

没有混淆逻辑很清晰的Scratch工程文件:

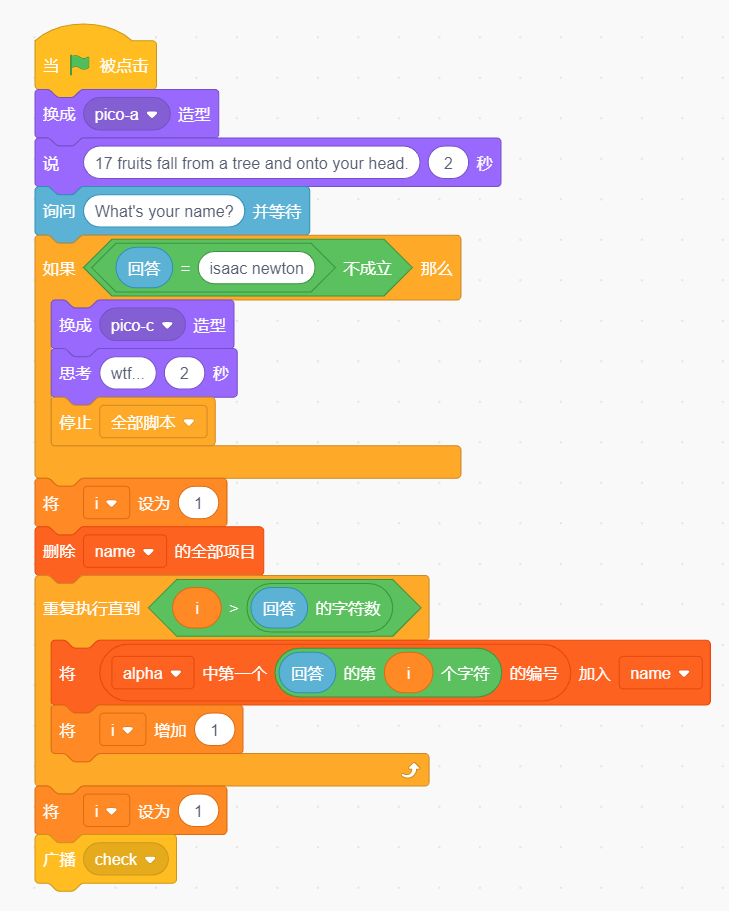
image-20231204194621457

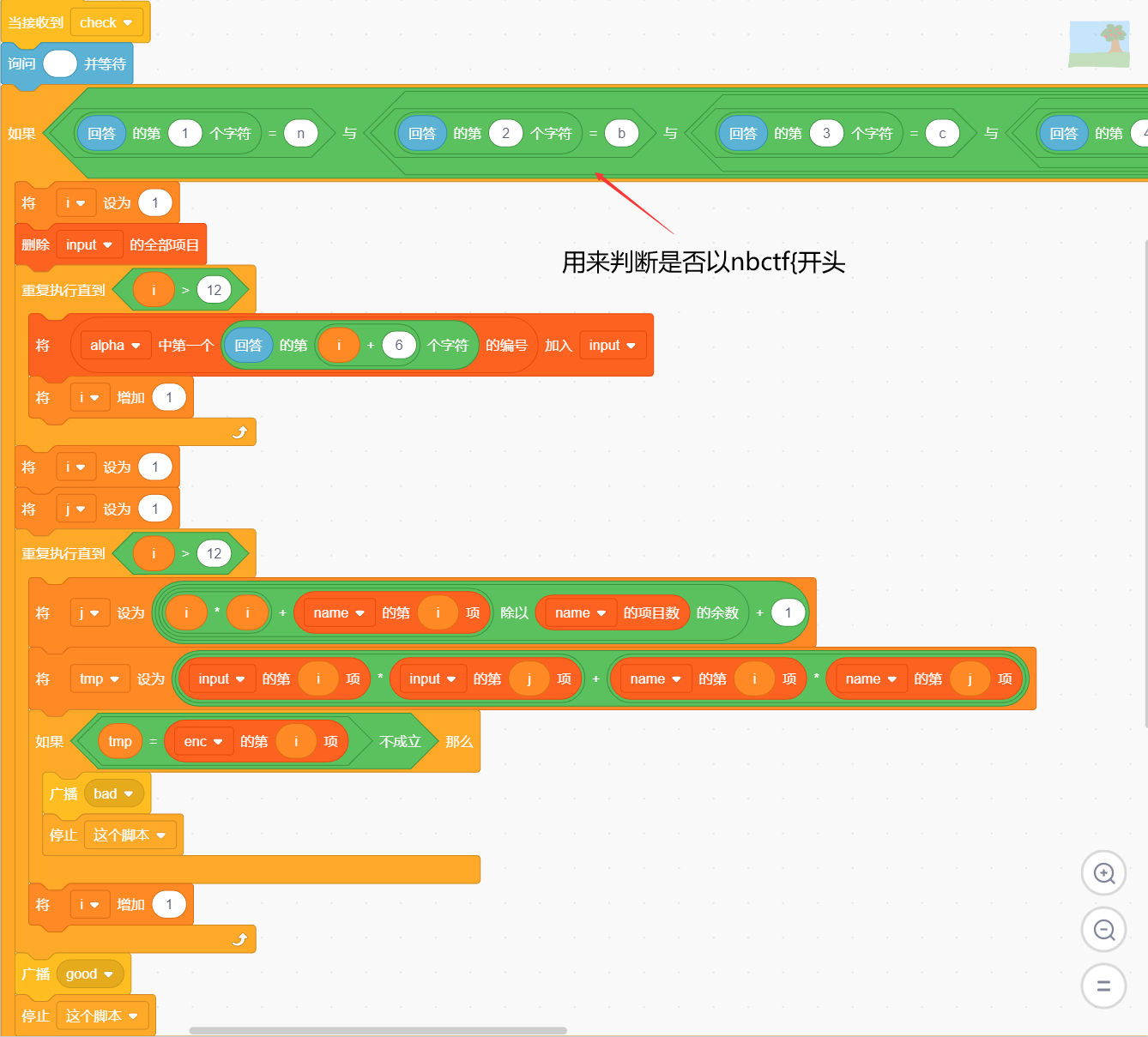
image-20231204195439820

alpha和enc也都给出了 唯一的问题是最后需要解方程 这里用z3求解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from z3 import *

name = [29,26,7,7,6,0,10,32,4,3,21,10]
alpha = 'zvtwrca57n49u2by1jdqo6g0ksxfi8pelmh3'
enc = [902,764,141,454,207,51,532,1013,496,181,562,342]
j = []
for i in range(1, 13):
    j.append((i * i + name[i - 1]) % len(name))
factor = []
for i in range(12):
    factor.append(name[i] * name[j[i]])
enc = [enc[i] - factor[i] for i in range(12)]
vi = IntVector('vi', 12)
s = Solver()
for i in range(12):
    s.add(vi[i] * vi[j[i]] == enc[i])
result = s.check()
if result == sat:
    m = s.model()
    vi_values = [m[vi[i]].as_long() for i in range(12)]
    for each in vi_values:
        print(each, end=', ')
else:
    print('No solution')
# [17, 14, 33, 32, 3, 3, 36, 5, 28, 17, 11, 12]
intput = [17, 14, 33, 32, 3, 3, 36, 5, 28, 17, 11, 12]
print("\nnbctf{", end = '')
for each in intput:
    print(alpha[each - 1], end = '')
print("}")
# nbctf{12lett3rf149}

Twostep | 构式加密

题如其名 用了类似两步舞的加密方式 有一种独特的美感(但是逆向的时候感觉不出来😡)

用DIE打开附件 64位ELF无壳

主函数的逻辑依然很简单:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
__int64 __fastcall main(int a1, char **a2, char **a3)
{
  __int64 v3; // rax
  __int64 v4; // rax
  __int64 v6; // rax
  char input[40]; // [rsp+0h] [rbp-40h] BYREF
  unsigned __int64 v9; // [rsp+28h] [rbp-18h]

  v9 = __readfsqword(0x28u);
  std::string::basic_string(input, a2, a3);
  v3 = print(&std::cout, "C'mon y'all let's boogie!\n> ");
  println(v3, &std::flush<char,std::char_traits<char>>);
  std::operator>><char>(&std::cin, input);
  if ( std::string::length(input) == 57 && (v4 = std::string::c_str(input), encrypto(v4)) )
    v6 = print(&std::cout, "Yeehaw!");
  else
    v6 = print(&std::cout, "Aww shucks!");
  println(v6, &std::endl<char,std::char_traits<char>>);
  std::string::~string(input);
  return 0LL;
}

但是打开encrypto()时出现了IDA无法反编译的错误 发现是text.40168C处发生了call无法解析的错误我们去看看这个铸币是怎么回事

1
.text:000000000040168B FF D0                         call    rax

上下文也看不出rax存放的是固定的某个函数还是什么 不要紧我们先nop掉它 顺利反编译了encrypto() 发现它调用了encrypto2()(这些都是我自己命名的) 打开encrypto2()发现它调用了encrypto()… 这就是”两步舞”的含义 不管 先分析两个函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
__int64 __fastcall encrypto(_BYTE *input_6)
{
  __int64 result; // rax
  char v2; // [rsp+19h] [rbp-A7h]
  __int16 v3; // [rsp+1Ah] [rbp-A6h]
  __int16 v4; // [rsp+1Ch] [rbp-A4h]
  __int16 v5; // [rsp+1Eh] [rbp-A2h]
  unsigned __int64 i; // [rsp+20h] [rbp-A0h]
  unsigned __int64 k; // [rsp+20h] [rbp-A0h]
  __int64 v8; // [rsp+20h] [rbp-A0h]
  unsigned __int64 m; // [rsp+20h] [rbp-A0h]
  unsigned __int64 j; // [rsp+28h] [rbp-98h]
  _BYTE *v11; // [rsp+30h] [rbp-90h]
  _BYTE *v12; // [rsp+30h] [rbp-90h]
  _BYTE *v13; // [rsp+30h] [rbp-90h]
  __int16 v14[4]; // [rsp+38h] [rbp-88h]
  __int64 v15[6]; // [rsp+40h] [rbp-80h]
  __int64 v16[8]; // [rsp+70h] [rbp-50h]
  __int16 v17; // [rsp+B6h] [rbp-Ah]
  unsigned __int64 v18; // [rsp+B8h] [rbp-8h]

  v18 = __readfsqword(0x28u);
  v14[0] = 18440;
  v14[1] = 3136;
  v14[2] = 18444;
  v14[3] = 16524;
  v16[0] = 1LL;
  v16[1] = 16LL;
  v16[2] = 32LL;
  v16[3] = 512LL;
  v16[4] = 1024LL;
  v16[5] = 2048LL;
  v16[6] = 0x2000LL;
  v16[7] = 0x4000LL;
  v15[0] = 177LL;
  v15[1] = 166LL;
  v15[2] = 183LL;
  v15[3] = 182LL;
  v15[4] = 177LL;
  v15[5] = 173LL;
  v17 = 170;
  switch ( var )
  {
    case 0LL:
      if ( *input_6 == 110
        && input_6[1] == 98
        && input_6[2] == 99
        && input_6[3] == 116
        && input_6[4] == 102
        && input_6[5] == 123 )
      {
        result = encrypto2(input_6 + 6);
      }
      else
      {
        result = 0LL;
      }
      break;
    case 1LL:
      v11 = check1_var_add(input_6);
      for ( i = 0LL; i <= 3; ++i )
      {
        v2 = v11[i];
        v4 = 0;
        for ( j = 0LL; j <= 3; ++j )
        {
          v4 |= (v2 & 3) << (4 * j + 2);
          v2 >>= 2;
        }
        if ( v4 != v14[i] )
          return 0LL;
      }
      result = encrypto2(input_6);
      break;
    case 3LL:
      v12 = check1_var_add(input_6);
      for ( k = 0LL; k <= 4; ++k )
        data[k] = v12[k];
      result = encrypto2(input_6);
      break;
    case 6LL:
      v3 = *check1_var_add(input_6);
      v8 = 0LL;
      while ( v3 )
      {
        v5 = v3 & -v3;
        if ( v8 == 8 )
          return 0LL;
        if ( v16[v8] == v5 )
          ++v8;
        v3 ^= v5;
      }
      result = v8 == 8 && encrypto2(input_6);
      break;
    case 8LL:
      v13 = check1_var_add(input_6);
      for ( m = 0LL; m <= 5; ++m )
        LOBYTE(v17) = v13[m] ^ v15[m];
      result = 1LL;
      break;
    default:
      result = 0LL;
      break;
  }
  return result;
}

//================================================

__int64 __fastcall encrypto2(_BYTE *input)
{
  __int64 result; // rax
  unsigned __int64 i; // [rsp+18h] [rbp-E8h]
  unsigned __int64 j; // [rsp+18h] [rbp-E8h]
  unsigned __int64 k; // [rsp+18h] [rbp-E8h]
  __int64 v5; // [rsp+20h] [rbp-E0h]
  _BYTE *v6; // [rsp+28h] [rbp-D8h]
  _BYTE *v7; // [rsp+28h] [rbp-D8h]
  _BYTE *v8; // [rsp+28h] [rbp-D8h]
  _BYTE *v9; // [rsp+28h] [rbp-D8h]
  __int64 v10[6]; // [rsp+30h] [rbp-D0h]
  __int64 v11[6]; // [rsp+60h] [rbp-A0h]
  __int64 v12[6]; // [rsp+90h] [rbp-70h]
  __int64 v13[8]; // [rsp+C0h] [rbp-40h]

  v13[7] = __readfsqword(0x28u);
  v13[0] = 0xD4F3LL;
  v13[1] = 0x3D49LL;
  v13[2] = 0x107BLL;
  v13[3] = 0xC479LL;
  v13[4] = 0xAA84LL;
  v13[5] = 0x9807LL;
  v10[0] = 0x394CLL;
  v10[1] = 24063LL;
  v10[2] = 37349LL;
  v10[3] = 50716LL;
  v10[4] = 61563LL;
  v11[0] = 1843061LL;
  v11[1] = 222420LL;
  v11[2] = 5184810LL;
  v11[3] = 4590105LL;
  v11[4] = 2184197LL;
  v5 = 0LL;
  v12[0] = 1073741834LL;
  v12[1] = 2415919110LL;
  v12[2] = 939524099LL;
  v12[3] = 536870913LL;
  v12[4] = 1845493760LL;
  switch ( var )
  {
    case 0LL:
      v6 = check1_var_add(input);
      if ( (*v6 ^ 0x5F) == v6[1]
        && (v6[1] ^ 0x75) == v6[2]
        && (v6[2] ^ 0x12) == v6[3]
        && (v6[3] ^ 0x38) == *v6
        && *v6 == 0x6C )
      {
        result = encrypto(input);
      }
      else
      {
        result = 0LL;
      }
      break;
    case 2LL:
      v7 = check1_var_add(input);
      for ( i = 0LL; i <= 4; ++i )
      {
        if ( v13[i] + v13[i + 1] * v7[i] != v11[i] )
          return 0LL;
      }
      result = encrypto(input);
      break;
    case 4LL:
      v8 = check1_var_add(input);
      for ( j = 0LL; j <= 4; ++j )
      {
        v5 += data[j] + (v8[j] << 7);
        if ( v5 != v10[j] )
          return 0LL;
      }
      result = encrypto2(input);
      break;
    case 5LL:
      v9 = check1_var_add(input);
      for ( k = 0LL; k <= 4; ++k )
      {
        if ( v12[k] != ((v9[k] >> (k + 3)) | (v9[k] << (32 - (k + 3)))) )
          return 0LL;
      }
      result = encrypto(input);
      break;
    case 7LL:
      qword_404308 = *check1_var_add(input);
      result = *&qword_404308 == 3.325947034342098e151 && encrypto(input);
      break;
    default:
      result = 0LL;
      break;
  }
  return result;
}

//================================================

_BYTE *__fastcall check1_var_add(_BYTE *input_6)
{
  __int64 v1; // rax
  __int64 v2; // rax
  __int64 v5; // [rsp+18h] [rbp-8h]

  v1 = var++;
  v5 = word_404090[v1];                         // 下划线数量
  while ( v5 )
  {
    if ( *++input_6 == '}' || !*input_6 )       // *(input + 1) == '}' || !*input
                                                // input++
    {
      v2 = print(&std::cout, "Aww shucks!");
      println(v2, &MEMORY[0x7F456B738680]);
      exit(1);
    }
    if ( *input_6 == '_' )
    {
      ++input_6;
      --v5;
    }
  }
  return input_6;
}

两个加密函数都调用了的check1_var_add(_BYTE *input_6)实际上是一个通过当前”步数”(var 对应每个case块的加密)来返回当前加密的单词在整个flag中的位置(flag中每个单词用_分割) 动态调试时发现步数和位置的对应关系如下:

1
2
index:    4, 7, 2, 0, 3, 6, 5, 1, 8
var:    0, 1, 2, 3, 4, 5, 6, 7, 8

其实得到了这些信息后一步步攻破每个case块的加密即可 但看出check1_var_add(_BYTE *input_6)的作用实际上也是一个 以下给出每个加密块对应的解密脚本:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
# case 1:
flag = []
flag.append(0x6C)
flag.append(flag[0] ^ 0x5F)
flag.append(flag[1] ^ 0x75)
flag.append(flag[2] ^ 0x12)
flag.append(flag[3] ^ 0x38)
flag[0] = [chr(val) for val in flag]
# print(flag)
# l3FTl __5
# l3FT  __5

# case 2:
flag = [None] * 4
flag[0] = 0x4808
flag[1] = 0xc40
flag[2] = 0x480c
flag[3] = 0x408c
flag = [val >> 2 for val in flag]
flag = [chr(val & 3 | ((val >> 4) & 3) << 2 | ((val >> 8) & 3) << 4 | ((val >> 12) & 3) << 6) for val in flag]
# print(flag)
# b4cK __8

# case 3:
flag = [None] * 5
flag[0] =  0x1c1f75
flag[1] =  0x364d4
flag[2] =  0x4f1d2a
flag[3] =  0x460a19
flag[4] =  0x215405
key = [None] * 6
key[0] = 0xD4F3
key[1] = 0x3D49
key[2] = 0x107B
key[3] = 0xC479
key[4] = 0xAA84
key[5] = 0x9807
flag = [chr(int((flag[i] - key[i]) / key[i + 1])) for i in range(5)]
# print(flag)
# r1gh7 __3

# case 4 & 5:
enc = [None] * 5
enc[0] = 0x394C
enc[1] = 24063
enc[2] = 37349
enc[3] = 50716
enc[4] = 61563
copy = [val for val in enc]
for i in range(5):
    if i > 0:
        enc[i] -= copy[i - 1]
    print(chr(enc[i] >> 7), chr(enc[i] % 0x80))
# r L
# I 3
# g f
# h 7
# T _
# index:
# 4 1

# case 5:
flag = ''
enc = [None] * 100
enc[0] = 0x4000000a
enc[1] = 0x90000006
enc[2] = 0x38000003
enc[3] = 0x20000001
enc[4] = 0x6e000000

for i in range(5):
    flag += chr(enc[i] >> (32 - (i + 3)) | enc[i] << (i + 3) & 0xFF)
# print(flag)
# RigH7 __7

# case 6:
enc[0] = 1
enc[1] = 0x10
enc[2] = 0x20
enc[3] = 0x200
enc[4] = 0x400
enc[5] = 0x800
enc[6] = 0x2000
enc[7] = 0x4000
# print(chr(0x31), chr(0x6E))
# 1n __6

# case 7:
x = 0x5F64523477723066
for i in range(8):
    print(chr((x >> i * 8) & 0XFF), end = '')
# f0rw4Rd_ __2

最后问题来了 实际上call rax对应到伪代码就是

1
2
3
4
5
6
7
case 8LL:
      v13 = check1_var_add(input_6);
      for ( m = 0LL; m <= 5; ++m )
        LOBYTE(v17) = v13[m] ^ v15[m];
        (&v17)();		//调用v17
      result = 1LL;
      break;

那么其实rax是根据计算得到的不确定的值 但是原来的程序少了这一步貌似也是甚至就应该这样照常运行 那么什么时候call rax相当于什么都没做呢?

  1. call $+5 ;花指令
  2. call rax ;rax -> ret 调用后立即返回

第一种显然不太可能 那就是当rax == retn(C3)时了! 于是写出最后一块解密脚本:

1
2
3
4
5
6
7
8
9
10
11
# case 8:
enc = [None] * 6
enc[0] = 0xb1
enc[1] = 0xa6
enc[2] = 0xb7
enc[3] = 0xb6
enc[4] = 0xb1
enc[5] = 0xad
for each in enc:
    print(chr(each ^ 0xC3 & 0xFF), end='')
# return __9

最后组合起来得到最终flag:nbctf{L3f7_f0rw4Rd_r1gh7_rIghT_l3FT_1n_RigH7_b4cK_return}

(其实nbctf{L3f7_f0rw4Rd_r1gh7_rIghT_l3FTl_1n_RigH7_b4cK_return也能让程序返回正确的提示 但显然是非预期解)

wee-woo | 栈机逆向

UIUA研究